前言
众所周知,C语言的数据类型有好几种,而其都有大小限制,比如说常见的长整型,其占用内存4个字节,可以储存的数字的大小为-2147483648~2147483647,但是在编程的时候,我们有可能会碰到非常非常大的数字,其可能超过长整型的最大上线导致数据溢出,所以我们得想一个方法来让C语言能够储存并且·处理超大数字。

我这篇博客文章便提供了一个思路,将超大的数字作为数组来进行处理,并自行编写各个数组之间的加减乘除之间的运算
加法处理
首先是加法,小学也是先讲解加法的,我们这篇主要用来讨论正整数的大数字之间的运算,如果是有小数或者负数请修改相应的代码即可。
加法的思路,就按照我们一般手工计算的思路,
首先从最末尾进行运算,大于十的进一位便可以了
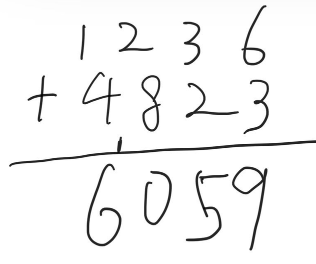
代码如下,代码中的数组a和b便是要相加的两个大数字,数组c即为计算的结果,可以根据需要将代码定义为函数。
//C语言数字超过上限的解决方案(通过数组来处理)
#include<stdio.h>
int main()
{
int a[20] = {0,0,0,0,0,1,2,3,4,5,6,7,8,9,2,3,1,4,2,2}; //第一个数字
for (int i=0;i<=19;i++) //输出一下
{
printf("%d", a[i]);
}
printf("\n");
int b[20] = { 0,0,0,0,3,5,3,1,5,9,7,5,6,7,8,4,2,4,8,1 }; //第二个数字
for (int i = 0; i <= 19; i++) //输出一下
{
printf("%d", b[i]);
}
printf("\n");
int c[20] = {0}; //定义结果的数组
int temp = 0; //进位符
for (int i = 0; i <= 19; i++)
{
if (temp == 0) //判断是否要进位
{
if (a[19 - i] + b[19 - i] < 10)
{
c[19 - i] = a[19 - i] + b[19 - i];
}
else
{
c[19 - i] = a[19 - i] + b[19 - i] - 10;
temp = 1;
}
}
else
{
if (a[19 - i] + b[19 - i] + 1 < 10)
{
c[19 - i] = a[19 - i] + b[19 - i] + 1;
temp = 0;
}
else
{
c[19 - i] = a[19 - i] + b[19 - i] + 1 - 10;
temp = 1;
}
}
}
for (int i = 0; i <= 19; i++) //输出结果
{
printf("%d", c[i]);
}
printf("\n");
return 0;
}减法
解决完加法,那么肯定要来解决减法,加法跟减法类似,只不过是退位而不是进位,但是下方给的代码是无法处理负数的,具体处理负数的情况请对源代码进行稍加修改,这里的代码只是用来提供思路的。
//C语言数字超过上限的解决方案(通过数组来处理)(a-b)
#include<stdio.h>
int main()
{
int a[20] = {0,0,0,0,7,1,2,3,4,5,6,7,8,9,2,3,1,4,2,2}; //第一个数字
for (int i=0;i<=19;i++) //输出一下
{
printf("%d", a[i]);
}
printf("\n");
int b[20] = { 0,0,0,0,3,5,3,1,5,9,7,5,6,7,8,4,2,4,8,1 }; //第二个数字
for (int i = 0; i <= 19; i++) //输出一下
{
printf("%d", b[i]);
}
printf("\n");
int c[20] = {0}; //定义结果的数组
int temp = 0; //进位符
for (int i = 0; i <= 19; i++)
{
if (temp == 0) //判断是否要退位
{
if (a[19 - i] - b[19 - i] >= 0)
{
c[19 - i] = a[19 - i] - b[19 - i];
}
else
{
c[19 - i] = a[19 - i] - b[19 - i] + 10;
temp = 1;
}
}
else
{
if (a[19 - i] - b[19 - i] - 1 >= 0)
{
c[19 - i] = a[19 - i] - b[19 - i] - 1;
temp = 0;
}
else
{
c[19 - i] = a[19 - i] - b[19 - i] - 1 + 10;
temp = 1;
}
}
}
for (int i = 0; i <= 19; i++) //输出结果
{
printf("%d", c[i]);
}
printf("\n");
return 0;
}乘法
乘法就比较复杂了,也是按照我们人手工计算的方法
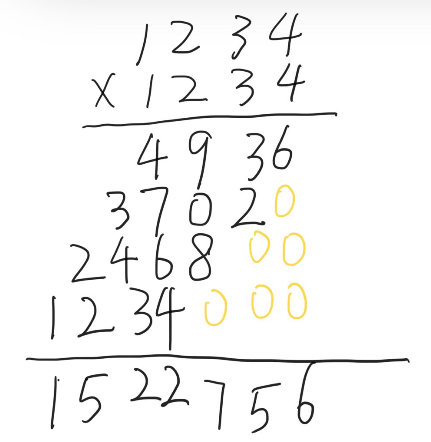
代码实现思路:被乘数先乘以乘数的最后一位,然后被乘数再乘以乘数的倒数第二位然后乘以一个十,一次类推,将刚刚上述的式子计算结果加在一起,输出结果即可
编写代码的时候要注意数据的大小,可能两个数子相乘会出现大于我们使用的数组的大小的情况,代码中要做好异常处理
//C语言数字超过上限的解决方案(通过数组来处理)
#include<stdio.h>
int main()
{
int a[20] = {0,0,0,0,0,0,0,0,0,0,0,0,1,2,3,4,5,6,7,8}; //第一个数字
for (int i=0;i<=19;i++) //输出一下
{
printf("%d", a[i]);
}
printf("\n");
int b[20] = { 0,0,0,0,0,0,0,0,0,0,0,0,1,2,3,4,5,6,7,8 }; //第二个数字
for (int i = 0; i <= 19; i++) //输出一下
{
printf("%d", b[i]);
}
printf("\n");
int c[20] = {0}; //定义结果的数组
int temp[20] = { 0 };
int q = 0; //要进位的数字
for (int i = 0; i <= 19; i++)
{
for (int x = 0; x <= 19; x++)
{
if (q == 0)
{
if (a[19 - x] * b[19-i] < 10)
{
temp[19 - x] = a[19 - x] * b[19 - i];
}
else
{
temp[19 - x] = (a[19 - x] * b[19 - i]) % 10;
q = (a[19 - x] * b[19 - i] - (a[19 - x] * b[19 - i]) % 10) / 10;
}
}
else
{
if (a[19 - x] * b[19 - i] + q < 10)
{
temp[19 - x] = a[19 - x] * b[19 - i] + q;
q = 0;
}
else
{
temp[19 - x] = ((a[19 - x] * b[19 - i]) + q) % 10;
q = ((a[19 - x] * b[19 - i] + q) - ((a[19 - x] * b[19 - i] + q) % 10)) / 10;
}
}
}
//先将结果后加零(小心溢出哦)(0的数量第一个加0个零,第二个加1个依次类推)
//先判断下是否会溢出
int Conter = 0;
while (temp[Conter] == 0)
{
Conter = Conter + 1;
}
if (Conter == 20) continue; //全零直接跳过
if (i > Conter)
{
printf("抱歉超过最大计算上限,最大结果输出为20位,请修改程序源代码来支持更多的位数\n");
return -1;
}
//然后往临时变量后面加零
Conter = i;
for (;Conter >0; Conter --)
{
for (int Bubble_time = 0;Bubble_time < 19; Bubble_time ++)
{
temp[Bubble_time] = temp[Bubble_time + 1];
}
temp[19] = 0;
}
//接下来将这些变量加在一起
//这里直接用加法的代码,但是注意下记得修改变量名避免出错
int ADD_temp = 0; //进位符
for (int ADD_i = 0; ADD_i <= 19; ADD_i++)
{
if (ADD_temp == 0) //判断是否要进位
{
if (c[19 - ADD_i] + temp[19 - ADD_i] < 10)
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i];
}
else
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i] - 10;
ADD_temp = 1;
}
}
else
{
if (c[19 - ADD_i] + temp[19 - ADD_i] + 1 < 10)
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i] + 1;
ADD_temp = 0;
}
else
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i] + 1 - 10;
ADD_temp = 1;
}
}
}
}
for (int q = 0; q <= 19; q++) //输出结果
{
printf("%d", c[q]);
}
}除法
除法便是最复杂的了,首先仍然看手工计算的草稿
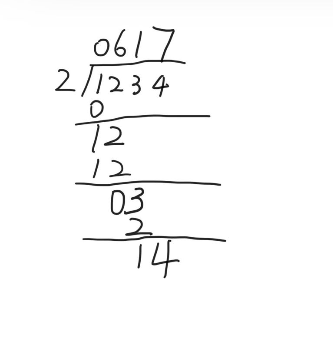
按照手工计算的思路,便可以写出下方的代码
由于其中涉及了加减乘除,所以说已经将加减乘除的过程分辨定义为了函数,这样简化了代码,也方便了调用,调用函数返回的是一个数组指针,如同加法那里的代码一样,a为被除数,b为除数。
还有一点要注意的,假如这个除法的结果除不尽的话,函数会如同正常c除法一样返回取整的数字,下方代码并未提供取余数的函数,您可以自己添加
#include<stdio.h>
//加法的函数,返回数组指针
int *add(int a[20],int b[20])
{
static int c[20] = { 0 };
for (int i = 0; i <= 19; i++)
{
c[i] = 0;
}//定义结果的数组
int temp = 0; //进位符
for (int i = 0; i <= 19; i++)
{
if (temp == 0) //判断是否要进位
{
if (a[19 - i] + b[19 - i] < 10)
{
c[19 - i] = a[19 - i] + b[19 - i];
}
else
{
c[19 - i] = a[19 - i] + b[19 - i] - 10;
temp = 1;
}
}
else
{
if (a[19 - i] + b[19 - i] + 1 < 10)
{
c[19 - i] = a[19 - i] + b[19 - i] + 1;
temp = 0;
}
else
{
c[19 - i] = a[19 - i] + b[19 - i] + 1 - 10;
temp = 1;
}
}
}
return c;
}
//减法的函数,返回数组指针(a-b)
int* sub(int a[20], int b[20])
{
static int c[20] = { 0 }; //定义结果的数组
for (int i = 0; i <= 19; i++)
{
c[i] = 0;
}
int temp = 0; //进位符
for (int i = 0; i <= 19; i++)
{
if (temp == 0) //判断是否要退位
{
if (a[19 - i] - b[19 - i] >= 0)
{
c[19 - i] = a[19 - i] - b[19 - i];
}
else
{
c[19 - i] = a[19 - i] - b[19 - i] + 10;
temp = 1;
}
}
else
{
if (a[19 - i] - b[19 - i] - 1 >= 0)
{
c[19 - i] = a[19 - i] - b[19 - i] - 1;
temp = 0;
}
else
{
c[19 - i] = a[19 - i] - b[19 - i] - 1 + 10;
temp = 1;
}
}
}
return c;
}
// 乘法的函数,返回数组指针,返回NUll即为超出上限
int* rid(int a[20], int b[20])
{
static int c[20] = { 0 }; //定义结果的数组
for (int i = 0; i <= 19; i++)
{
c[i] = 0;
}
int temp[20] = { 0 };
int q = 0; //要进位的数字
for (int i = 0; i <= 19; i++)
{
for (int x = 0; x <= 19; x++)
{
if (q == 0)
{
if (a[19 - x] * b[19 - i] < 10)
{
temp[19 - x] = a[19 - x] * b[19 - i];
}
else
{
temp[19 - x] = (a[19 - x] * b[19 - i]) % 10;
q = (a[19 - x] * b[19 - i] - (a[19 - x] * b[19 - i]) % 10) / 10;
}
}
else
{
if (a[19 - x] * b[19 - i] + q < 10)
{
temp[19 - x] = a[19 - x] * b[19 - i] + q;
q = 0;
}
else
{
temp[19 - x] = ((a[19 - x] * b[19 - i]) + q) % 10;
q = ((a[19 - x] * b[19 - i] + q) - ((a[19 - x] * b[19 - i] + q) % 10)) / 10;
}
}
}
//先将结果后加零(小心溢出哦)(0的数量第一个加0个零,第二个加1个依次类推)
//先判断下是否会溢出
int Conter = 0;
while (temp[Conter] == 0)
{
Conter = Conter + 1;
}
if (Conter == 20) continue; //全零直接跳过
if (i > Conter)
{
printf("抱歉超过最大计算上限,最大结果输出为20位,请修改程序源代码来支持更多的位数\n");
return NULL;
}
//然后往临时变量后面加零
Conter = i;
for (; Conter > 0; Conter--)
{
for (int Bubble_time = 0; Bubble_time < 19; Bubble_time++)
{
temp[Bubble_time] = temp[Bubble_time + 1];
}
temp[19] = 0;
}
//接下来将这些变量加在一起
//这里直接用加法的代码,但是注意下记得修改变量名避免出错
int ADD_temp = 0; //进位符
for (int ADD_i = 0; ADD_i <= 19; ADD_i++)
{
if (ADD_temp == 0) //判断是否要进位
{
if (c[19 - ADD_i] + temp[19 - ADD_i] < 10)
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i];
}
else
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i] - 10;
ADD_temp = 1;
}
}
else
{
if (c[19 - ADD_i] + temp[19 - ADD_i] + 1 < 10)
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i] + 1;
ADD_temp = 0;
}
else
{
c[19 - ADD_i] = c[19 - ADD_i] + temp[19 - ADD_i] + 1 - 10;
ADD_temp = 1;
}
}
}
}
return c;
}
// 比较两个数组之间的大小是否大于 (1为真,0为假)
int a_big_then_b(int a[20],int b[20])
{
for (int i = 0; i <= 19; i++)
{
if (a[i] >b[i])
{
return 1;
}
if (a[i] < b[i])
{
return 0;
}
}
return 0;
}
// 比较两个数组之间是否相等(1为真,0为假)
int a_equal_then_b(int a[20], int b[20])
{
for (int i = 0; i <= 19; i++)
{
if (a[i] == b[i])
{
//printf("a[i] = b[i]");
}
else
{
return 0;
}
}
return 1;
}
//除法的函数,返回数组指针(a/b)
int* div(int a[20], int b[20])
{
static int c[20] = { 0 };
for (int i = 0; i <= 19; i++)
{
c[i] = 0;
}
int temp[20] = { 0 }; //向下留的余数的数组
for (int i = 0; i <= 19; i++)
{
//将之前的temp乘以10(进一位)
for (int Bubble_time = 0; Bubble_time < 19; Bubble_time++)
{
temp[Bubble_time] = temp[Bubble_time + 1];
}
temp[19] = 0;
int temp_compute[20] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,a[i]};
int* temp_point;
temp_point = add(temp, temp_compute);
for (int temp_counter = 0;temp_counter<=19;temp_counter++)
{
temp[temp_counter] = temp_point[temp_counter];
}
for (int x = 1; x <= 9; x++)
{
int temp_compute[20] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,x};
temp_point = rid(b,temp_compute);
if (a_big_then_b(temp_point,temp))
{
c[i] = x - 1;
int temp_compute[20] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,x-1};
temp_point = rid(b, temp_compute);
int* temp_point_2;
temp_point_2 = sub(temp, temp_point);
for (int temp_counter=0;temp_counter<=19;temp_counter++)
{
temp[temp_counter] = temp_point_2[temp_counter];
}
break;
}
if (a_equal_then_b(temp_point, temp))
{
c[i] = x;
for (int temp_counter=0;temp_counter<=19;temp_counter++)
{
temp[temp_counter] = 0;
}
break;
}
if (x == 9)
{
int temp_compute[20] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,a[i]};
temp_point = add(temp,temp_compute);
for (int temp_counter = 0; temp_counter <= 19; temp_counter++)
{
temp[temp_counter] = temp_point[temp_counter];
}
}
}
}
return c;
}
int main()
{
int a[20] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,3,4,5,7 }; //第一个数字
for (int i = 0; i <= 19; i++) //输出一下
{
printf("%d", a[i]);
}
printf("\n");
int b[20] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,2 }; //第二个数字
for (int i = 0; i <= 19; i++) //输出一下
{
printf("%d", b[i]);
}
printf("\n");
int* result;
result = div(a, b);
for (int i = 0; i <= 19; i++)
{
printf("%d",result[i]);
}
return 0;
}后记
上述算法只是其中的一个思路,可能不是最优的,并且代码中可能有缺陷,请指正,谢谢。