前言

上课时候老师讲算法的时候提到了一个有趣的问题，汉诺塔的最佳求解问题，这篇博文就讲述一下我研究这个的求解问题的过程

什么是汉诺塔问题

汉诺塔问题，源于印度古老传说。简单来说是这个样子的：某个地方有三个石塔，第一个从小到大摞着64片黄金圆盘。现在要把圆盘按大小顺序摆放在最后一个塔上。并规定，小圆盘上不能放大圆盘，在三个塔之间一次只能移动一个圆盘。请问如何实现？

算法思路

按照课本上所说的,“汉诺塔问题是一个典型的只有用递归的方法（而不能用其他方法）”来解决的问题。所以我们只能使用递归算法。

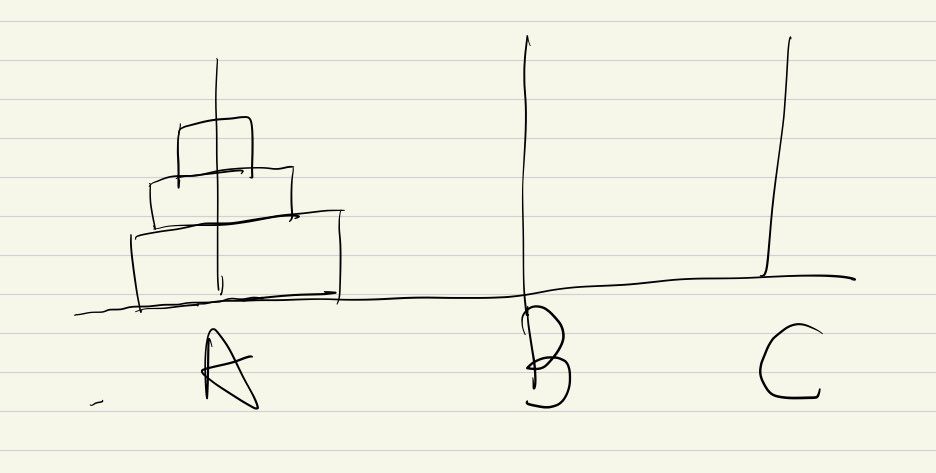
对于64个盘子的汉诺塔问题，我们可以将其进行转换，让其涉及到的盘子的数量逐级递减下去。在64个盘子的时候，我们可以将上面的63个盘子看作一个整体，即64个盘子可以看作独立的两个部分（原来的63个一起设为a和另外的一个设为b ）。

然后接下来就相当于两个盘子的问题了，就如下图所示，第一步将a挪到B处，第二步将b挪到C处，第三步将a挪到C处

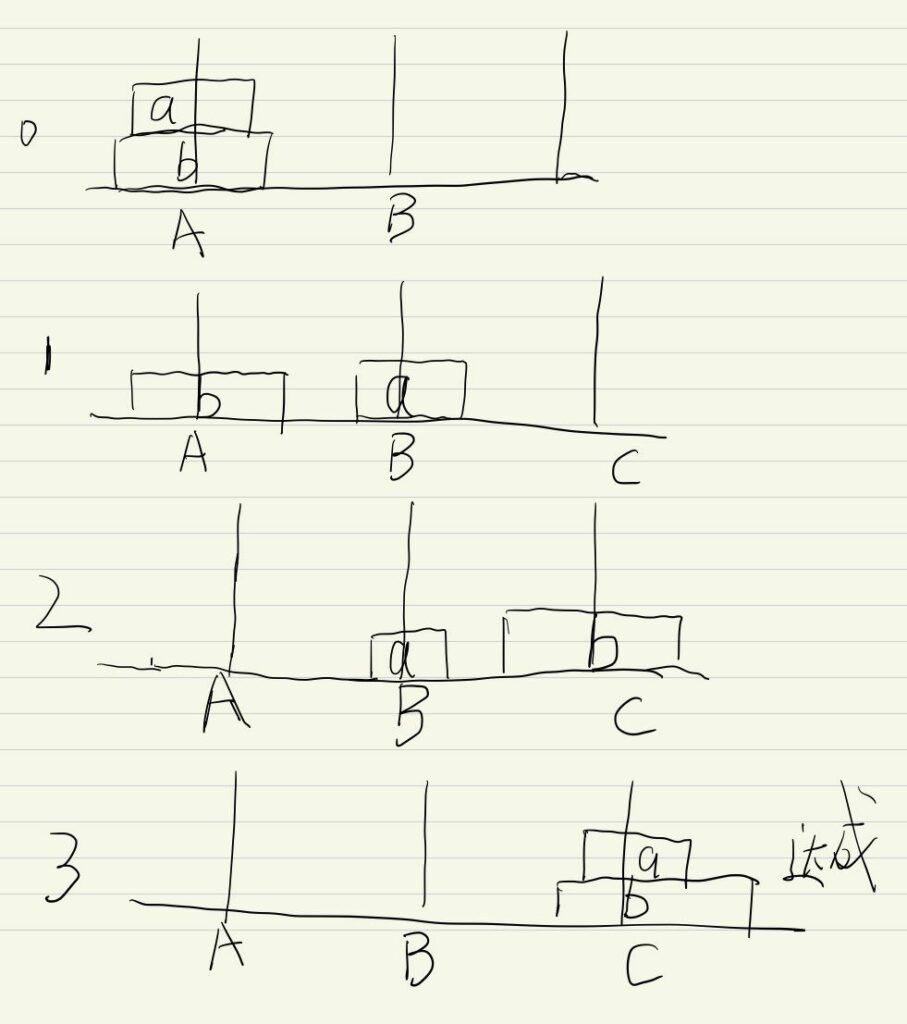
没弄懂？那么来看看3个盘子的问题，如下图

正常情况下是按照下图1~8的过程来的

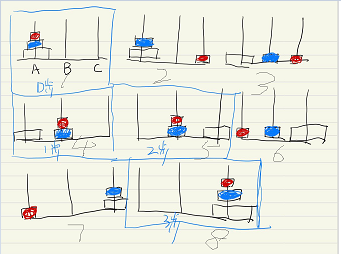
但是我们也可以将其看作两个盘子的问题，如图第1~3步（蓝色方框框住的），只不过第0步到第1步（蓝色方框框住的）的过程相当于两个盘子的问题，只不是是将蓝色与红色盘子从A柱子挪到B柱子而已，而第2步到第3步（蓝色方框框住的）也是相当于两个盘子，从B柱子搬到C柱子。总计7步，计算式为总步数 = （上一层的步数）+ 1 + （上一层的步数） = 2x上一层的步数 + 1 = 2 x 3 + 1 = 7步

接下来就是63个盘子的问题，而63个盘子的问题又可以看作62个盘子的问题,依次进行递归下去，直到两个盘子的问题。接下来就是列算式了

一个盘子最少需要1步

二个盘子最少需要3步

三个盘子最少需要7步

四个盘子最少需要15步

。。。。。。。。

第n个盘子最少需要前一个盘子数量的2n+1步

那么就是来列算是

总次数= 1 + 3 + 7 + ….. + 2n+1

= 2^n-1

计算得出结果，总计次数=18446744073709551615