定点整数与定点纯小数
首先就是定点整数与定点纯小数,计算机里面没有专门设置小数点,但是,我们可以默认在计算机里面的数字的某一个地方中有一个小数点,并且这个小数点的位置是固定不变的,这样,我们就有了定点数的概念。
首先就是定点整数。定点整数就是我们约定的(个人默认的)小数点在数值的最低位之后的数(即是整数)。
我们先了解电脑中如何存储定点数。如下图。
首先是无符号位的定点数在电脑中储存的样子

下面是有符号位的定点数在电脑中储存的样子
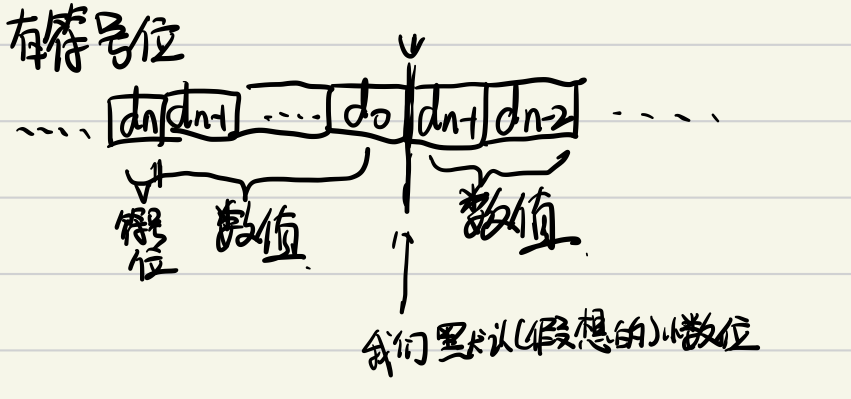
接下来我们就来一一解释上图中的各个部分
首先就是符号位,假如没有符号位的话,计算机是无法知道一个数字是正数还是负数,所以说有了符号位这个东西,符号位0表示正数,1表示负数。
接下来就是数值了,符号位置右边,我们假设的那个小数点的左边的数值表示整数部分的值,我们假设的小数点右边的数值则是定点数字的小数字部分。
然后就是讲定点整数与定点小数的差别,通俗的来讲定点整数是只有整数部分的定点数,定点小数是只有小数部分的定点数,当然,下面摘抄了我所用的课本关于定点整数与定点小数的定义
定点整数:如果小数点约定在数值的最低位之后,这时所有参与运算的数都是整数,即为定点整数。
定点纯小数:如果小数点约定在符号位和数值的最高位之间,这时所有参与运算的数的绝对值小于1,即为定点纯小数
摘自-《计算思维-计算学科导论》(唐培和-徐奕奕编著)第38-39面
浮点数
二进制的科学计数法
知晓了上述的信息之后,为了了解浮点数,我们现在要来了解一下二进制的科学计数法。
首先先回忆一下十进制的科学计数法,比如说1200按照十进制的科学计数法可以表示为0.12*10^4
那么对于任意一个二进制的数字,比如N,都可以类比十进制的科学计数法,写作这样的形式:t * 2^e
即 N=t*2^e
其中上式中的e被称为N的阶码,t被称为N的尾数(t为一个纯小数)。
举一个例子吧,1011可以转换为0.1011*2^4
当然你也可以写作2^4 * 0.1011 (本博文为了方便理解,就写作0.1011*2^4这个样子)
浮点数的表示与储存
了解这些,我们接下来就来看浮点数:
浮点数的概念:浮点数就是小数点可以浮动的数字
接下来就是计算机如何表示浮点数的了。我们已知二进制可以表示为t*2^e这个形式,浮点数就这样子表示:
(小提示,浮点数中分为单精度与双精度,单精度占用32位,双精度占用64位,本博文按照64位来解释)
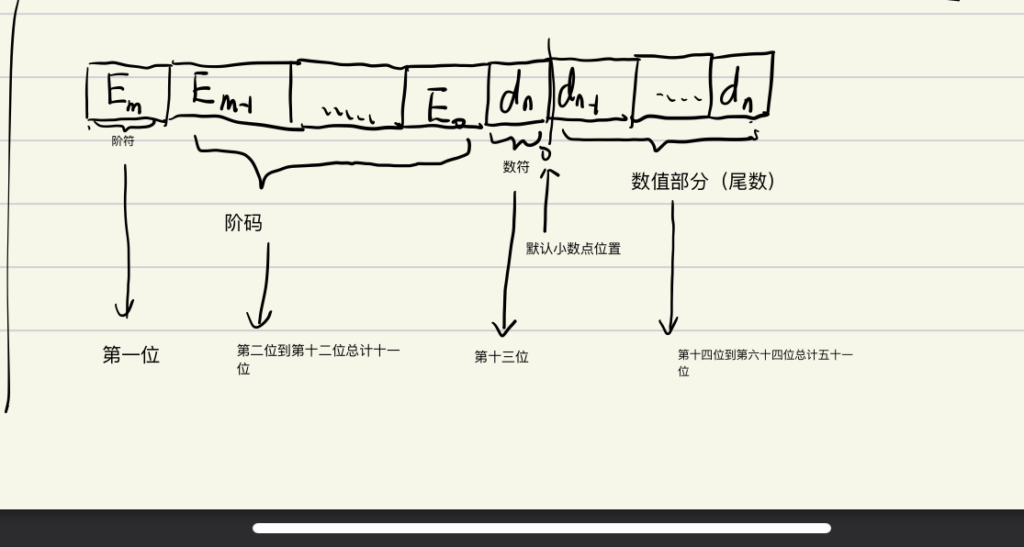
如上图
其中阶符与数符来决定正负,0为正,1为负,将上图中的值带入二进制的科学计数法中就可以表示出一个数字(有的数字在用科学计数法表示的时候可能会产生磨损,即超出范围的数据被四舍五入了,导致产生一点点偏差)
因为小数点所在的位置会跟着阶码的变化而变化(浮动),所以才叫做浮点数。