前言

首先，要开始学习这些进制之间如何互相转换，我们先要了解一下这些进制以及其包含的数字。具体见下表：

进制名称	进制英文名以及其简写名称	进制所包含的数字\字母
二进制	binary （bin）	0 1
八进制	octal （oct）	0 1 2 3 4 5 6 7
十进制	Decimal （dec）	0 1 2 3 4 5 6 7 8 9
十六进制	Hexadecimal （hex）	0 1 2 3 4 5 6 7 8 9 A B C D E F

基本了解了一下进制，接下来就要来了解进制之间的转换。

二进制等转换为十进制

首先就是了解二进制等进制如何转换为十进制，我们在这里使用一种叫做位权相加法的方法来进行转换。我们先以二进制转换为十进制为例子：

首先 假设有一个二进制数据 1010101

将其转化为十进制只需要这样：

十进制数值 = (1 * 2^6 )+(0 * 2^5)+( 1 * 2^4)+(0 * 2^3)+( 1* 2^2)+(0 * 2^1)+(1*2^0)=85

再举个例子：111001

十进制数值 = （1*2^5）+（1*2^4）+（1*2^3）+（0*2^2）+（0*2^1）+（1*2^0）= 57

假如包含小数的话，比如说

111.01

转换方式如下：

十进制数值 = （1*2^2）+（1*2^1）+（1*2^0）+（0*2^-1）+（0*2^-2）=7.25

其他进制转化为二进制的方法跟上面的过程相差不大，下方举个例子：

将8进制数值7231.24转化为十进制数值：

十进制数值 = （7*8^3) + （2*8^2) + （3*8^1) + （1*8^0) + （2*8^-1) + （4*8^-2) = 3737.3125

十进制等转化为二进制

接下来就是如何讲十进制数据转换为二进制数据

我们现在先以一个十进制整数 75和23为例子，如下图的过程

接下来就是含有小数的部分了，我们先以75.6875为例子

首先先是整数部分 75 根据上面先给的方法，整数部分二进制的结果为1001011

接下来是小数部分：0.6875转化为2进制

将整数部分与小数部分整合，得到75.6875的二进制数据为：1001011.1011

这里有一个要注意的地方，就是十进制转换为二进制可能是会有损失的，有转换磨损，比如说如下的数据

0.352这个数据，按照刚刚的转换方式，你会发现根本就乘不完，总是乘不到1这个数字，所以，老师说考试中题目都会给出所要求的精度，不会让你一直求下去。

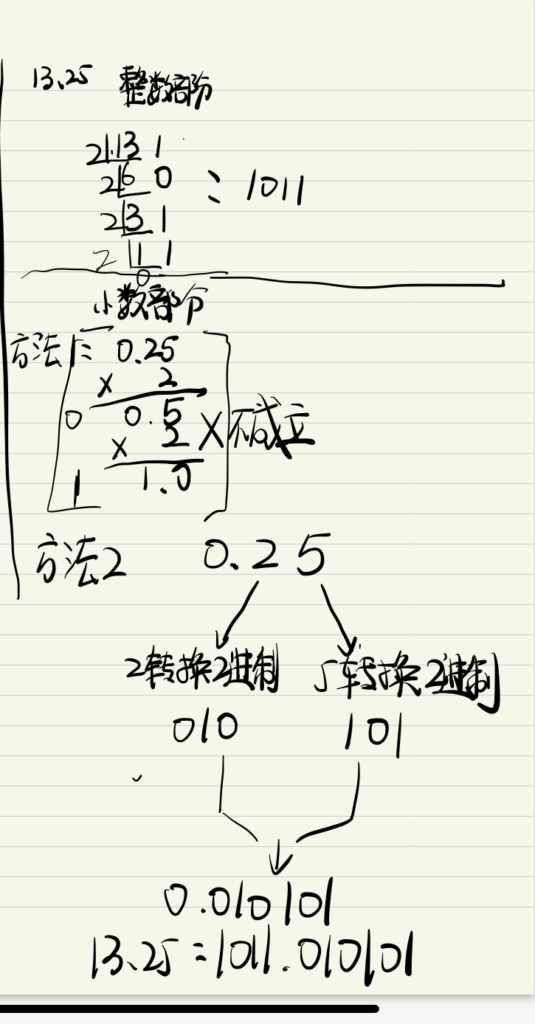
注意，刚刚上面这个求小数部分的转换方法只适用于10进制转换为2进制，对于其他进制转化为2进制是不行的，请看下面例子：

对于8进制转换为2进制，比如 13.25（八进制）这个数字，如下图操作：

总结

以上就是各个进制的转化方法了，假如要2进制转化为8进制，不妨先转化为10进制，当然也有其他的方法，这里不再一一赘述，谢谢阅读。